marco cognetta theoretically good with computers
Spending Too Much Time Optimizing LeetCode's Path With Maximum Gold
Note: You can also find my overview on LeetCode.
Note 2: I eventually improved on my original time. I added two new sections about it (brief update, updated optimizations).
Yesterday's LeetCode daily challenge was a brute-force backtracking problem, Path With Maximum Gold. To quickly explain, you have a grid () with at most 25 cells with a non-zero value denoting their amount of gold. Starting from any cell with gold, you can travel to any adjacent cells with gold (but not to the same cell twice), and your goal is to collect the maximum amount of gold possible.
This is a classic backtracking search problem, where you start at each cell, enumerate all valid paths, and pick the maximal one. The tight constraints of the problem support this approach, as brute forcing is likely to be within the time limits.
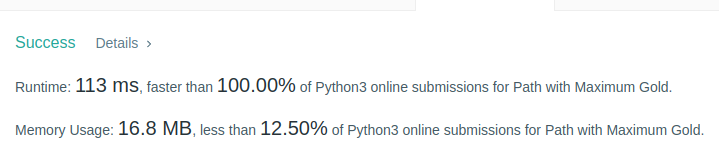
What I described above is the standard approach, and it does indeed solve the problem with a fairly clean implementation (see: the official LeetCode solutions). For reference, the basic LeetCode solution takes somewhere in the 3200-3600ms range to finish while the one I describe here is about 170ms[updated] 115ms, a >25x speedup.
This approach leaves a lot of performance on the table though, and I took a break from my normal LeetCode antics to go down the rabbit hole of trying to eke out as much speed as I could from a basic Python implementation.
Here is my journey:
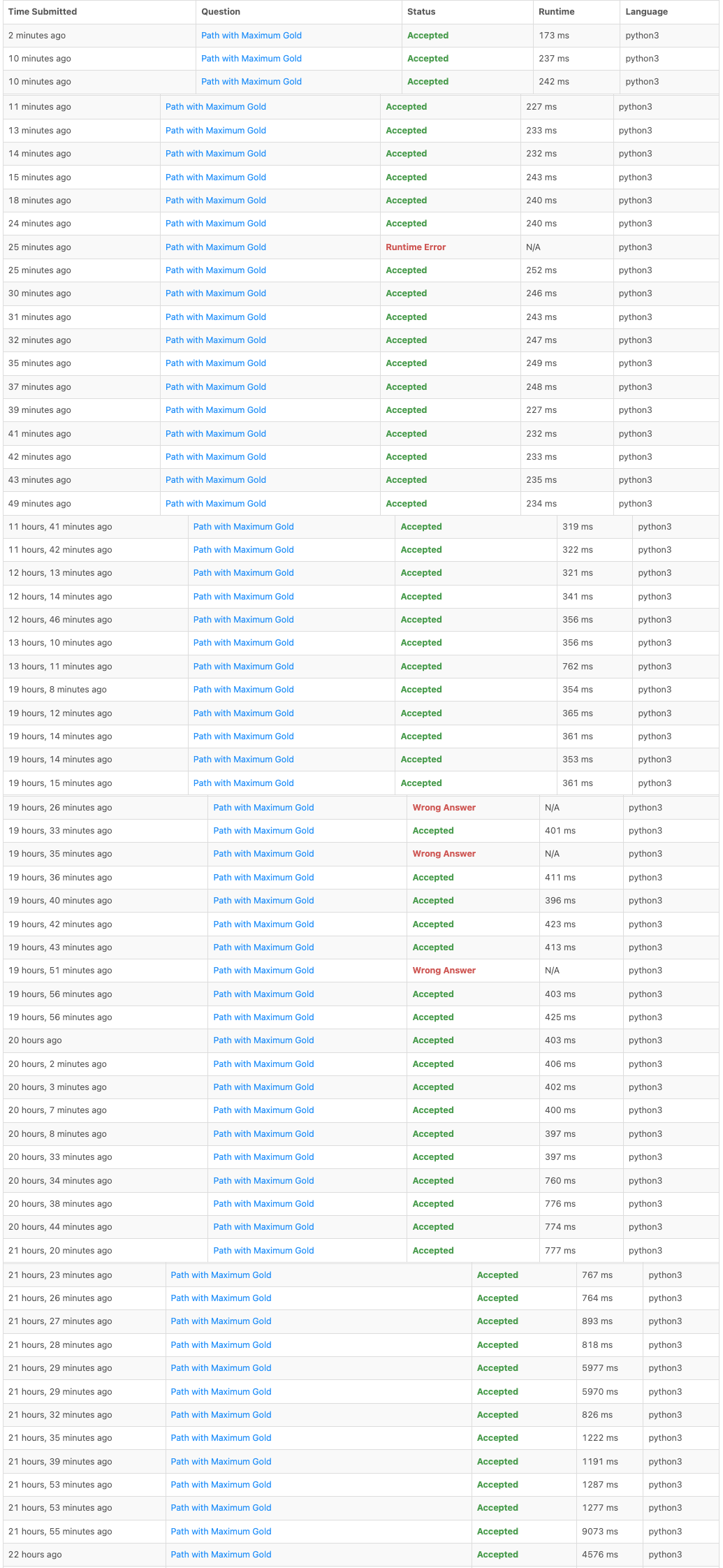
After which, I arrived at:

Update:
I little later I optimized the code mode and got down to 115ms, far better than the previous best time and easily the fastest on Leetcode. I added a section at the bottom of this post that covers these optimizations.
Optimizations
The main speedups came in the form of several heuristics that I was able to apply based on the different overall approach I took. Rather than brute forcing every viable cell, I took a slightly more structured approach of first finding all connected components of gold cells, then running brute force over each of them.
Breaking the graph into connected components unlocks basically all of the optimizations that were necessary to get to sub 400ms. In particular, short circuiting connected component searches.
We can short circuit in two ways:
If the current connected component's total gold value is less than the best path we have found so far (in another component)
If we have found a path in the current connected component that consumes the entire gold value (so no other path in the component can do better)
The first option enables another heuristic: searching connected components in order of their total gold value (under the assumption that higher value connected components will have higher value paths). In the end, this had negligible effect, but earlier during my optimizations it sped things up quite a bit.
The final optimization is a much more subtle one, and was what pushed the code from the 300ms range to sub 250ms (already at the 99.6 percentile), and then later to the sub 200ms range. The idea is that the only cells that can be at the end of a maximal path are those with 2 or fewer neighbors. The intuition is as follows: suppose we have some cell that has only one neighbor, so it is at the end of a "tail". There is no reason not to extend the path all the way to connect to that cell, since the value will strictly increase. Now suppose we have a cell with 3 or 4 neighbors. It either exists on a cycle (which must have a cell with 2 neighbors somewhere on it) or at least one of the neighbors is on a tail path (thus there is a cell with degree 1). Finally, consider a case where there is just a single cycle, so every cell has degree 2. Any cell in the cycle is a suitable starting point. So, if there is a degree 1 cell, we always take that, and if there are degree 3 or 4 cells, we can ignore those and use one of the degree 1 or 2 cells that must exist.
Restricting to only cells with degree at most 2 was enough to break the 250 range.
To break the 200ms barrier, one more trick was needed. One can extend the degree argument slightly to see that if there is are any degree 1 cells in the component, then at least one of them must be in the maximal path. Then we can search starting from all of the degree one cells first, and pick the maximum of their paths. If none exist, then we just search over all of the degree 2 cells as normal.
Overall, the core idea is that so much of this algorithm is dominated by the exhaustive search that any heuristic pruning is worth it.
The final code is as follows (with notation for the heuristics):
class Solution:
def getMaximumGold(self, grid: List[List[int]]) -> int:
R, C = len(grid), len(grid[0])
# helper function to get cell neighbors
def dirs(i, j):
for (di, dj) in ((0, 1), (0, -1), (1, 0), (-1, 0)):
n_i = i + di
n_j = j + dj
if 0 <= n_i < R and 0 <= n_j < C and grid[n_i][n_j]:
yield n_i, n_j
# helper function to get the maximum theoretical value of a
# connected component
def sum_component(component):
return sum(grid[r][c] for (r, c) in component)
# connected component finder
already_in_cc = [[False for _ in grid[0]] for _ in grid]
def cc(r, c):
component = [(r, c)]
queue = deque([(r, c)], maxlen=25)
already_in_cc[r][c] = True
while queue:
(i, j) = queue.popleft()
for (new_i, new_j) in dirs(i, j):
if not already_in_cc[new_i][new_j]:
already_in_cc[new_i][new_j] = True
component.append((new_i, new_j))
queue.append((new_i, new_j))
return component
# search over all non-zero cells for new components
components = []
for r in range(R):
for c in range(C):
if not already_in_cc[r][c] and grid[r][c]:
components.append(cc(r, c))
# given a component (and a current best score from another component)
# this searches over all possible paths by exahustive search
# it applies several heuristics, marked in line
def brute_force(component, cur_best):
# short circuit in the simple case where there is just a single
# cell in the component
if len(component) == 1: return grid[component[0][0]][component[0][1]]
# short circuit in the case where the maximum theoretical value
# for this component is less than a previously found best path
comp_sum = sum_component(component)
if comp_sum <= cur_best: return cur_best
# recursive exhaustive search helper function
def recur(r, c, score):
# we use a trick here to mark cells as visited during
# the search. storing the cell value, then setting it
# to 0 allows us to avoid costly data allocations and
# sharing during recursion
temp = grid[r][c]
score += temp
grid[r][c] = 0
best = score
for n_r, n_c in dirs(r, c):
best = max(best, recur(n_r, n_c, score))
grid[r][c] = temp
return best
# run the recursive search over valid starting cells (those with)
# degree 1 or 2
best = 0
# first check if there are any with degree 1, if so, one must appear
# in the maximal path
for (r, c) in [(r, c) for (r, c) in component if len(list(dirs(r, c))) == 1]:
best = max(best, recur(r, c, 0))
if best == comp_sum: return best
# if there weren't any, then we search over degree 2 cells as normal
if best == 0:
for (r, c) in [(r, c) for (r, c) in component if len(list(dirs(r, c))) == 2]:
best = max(best, recur(r, c, 0))
if best == comp_sum: return best
return best
# run the brute force search over all components
# we use a heuristic here to search in order of maximal theoretical
# value for the component
cur_best = 0
for c in sorted(components, key = sum_component, reverse=True):
cur_best = max(cur_best, brute_force(c, cur_best))
return cur_bestThe rest of the performance gains from my chart above were from minor things like reordering some code, reducing some nesting (in particular, I like to nest recursive inner functions), switching from sets to lists, etc.
However, one big jump (from ~700 to ~400ms) was due to me accidentally calling recur twice for each cell 🤦🏻♂️.
[Update] Final Optimizations
As mentioned, I was eventually able to go from the 170ms range to the 115ms range. To do this, I applied two more optimizations:
I padded the grid with zeros. Now, we never have to check if an index is inbounds, since no non-zero cell is on the border of the grid. This means we remove a check during the hottest loop of the function: the neighbor iterator.
I (manually) inlined the the
dirs(i, j)function (the one that finds neighbors) in all of the really hot loops. Since this is one of the most-run functions in the code, removing the overhead of calling the function is a big win.
The final code looks like this:
class Solution:
def getMaximumGold(self, grid: List[List[int]]) -> int:
# pad the grid with 0's so that non-zero cells are never on the border
grid = [[0]*(len(grid[0]) + 2)] + [[0] + r + [0] for r in grid] + [[0]*(len(grid[0]) + 2)]
R, C = len(grid), len(grid[0])
# helper function to get cell neighbors
def dirs(i, j):
for (n_i, n_j) in [(i, j+1), (i, j-1), (i+1, j), (i-1, j)]:
if grid[n_i][n_j]:
yield n_i, n_j
# helper function to get the maximum theoretical value of a
# connected component
def sum_component(component):
return sum(grid[r][c] for (r, c) in component)
# connected component finder
already_in_cc = [[False for _ in grid[0]] for _ in grid]
def cc(r, c):
component = [(r, c)]
queue = deque([(r, c)], maxlen=25)
already_in_cc[r][c] = True
while queue:
(i, j) = queue.popleft()
for (new_i, new_j) in dirs(i, j):
if not already_in_cc[new_i][new_j]:
already_in_cc[new_i][new_j] = True
component.append((new_i, new_j))
queue.append((new_i, new_j))
return component
# search over all non-zero cells for new components
components = []
for r in range(R):
for c in range(C):
if not already_in_cc[r][c] and grid[r][c]:
components.append(cc(r, c))
# given a component (and a current best score from another component)
# this searches over all possible paths by exahustive search
# it applies several heuristics, marked in line
def brute_force(component, cur_best):
# short circuit in the simple case where there is just a single
# cell in the component
if len(component) == 1: return grid[component[0][0]][component[0][1]]
# short circuit in the case where the maximum theoretical value
# for this component is less than a previously found best path
comp_sum = sum_component(component)
if comp_sum <= cur_best: return cur_best
# recursive exhaustive search helper function
def recur(r, c, score):
# we use a trick here to mark cells as visited during
# the search. storing the cell value, then setting it
# to 0 allows us to avoid costly data allocations and
# sharing during recursion
temp = grid[r][c]
score += temp
grid[r][c] = 0
best = score
# manually inline `dirs`
for n_r, n_c in [(r, c+1), (r, c-1), (r+1, c), (r-1, c)]:
if grid[n_r][n_c]: best = max(best, recur(n_r, n_c, score))
grid[r][c] = temp
return best
# run the recursive search over valid starting cells (those with)
# degree 1 or 2
best = 0
# first check if there are any with degree 1, if so, one must appear
# in the maximal path
for (r, c) in [(r, c) for (r, c) in component if len(list(dirs(r, c))) == 1]:
best = max(best, recur(r, c, 0))
if best == comp_sum: return best
# if there weren't any, then we search over degree 2 cells as normal
if best == 0:
for (r, c) in [(r, c) for (r, c) in component if len(list(dirs(r, c))) == 2]:
best = max(best, recur(r, c, 0))
if best == comp_sum: return best
return best
# run the brute force search over all components
# we use a heuristic here to search in order of maximal theoretical
# value for the component
cur_best = 0
for c in sorted(components, key = sum_component, reverse=True):
cur_best = max(cur_best, brute_force(c, cur_best))
return cur_best